NeurIPS 2021 | 旷视提出：空间集成 ——一种新颖的模型平滑机制

由于高昂的数据标注成本，无标签数据的利用获得了学术界和工业界越来越多的关注，涌现出不少优秀的半监督和自监督学习方法，例如 FixMatch, MoCo, BYOL 等，大幅缩小了半监督/自监督学习与全监督学习的性能差距。

其中，学生-老师框架+模型平滑技术已经成为半监督及自监督方法的一种流行范式。本文首先介绍了这种经典的范式，并从当前主流的基于时序的模型平滑机制出发，介绍了一种空间平滑方法——空间集成（Spatial Ensemble）。

1

学生-老师框架

以经典的半监督框架 Mean Teacher 为例，该方法采用了一种学生-老师框架（student-teacher framework）。

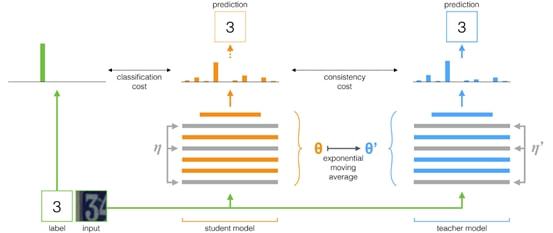
图1 Mean Teacher 框架示意图

如图 1 所示，该框架包含一个学生网络(student)和一个老师网络(teacher)。Teacher 为无标签数据生成类别伪标签监督信号,以引导 student 的学习。

在这个过程中，student 基于常规的梯度反向传播来进行更新，而 teacher 则借助于模型平滑技术（Model Smoothing)来进行更新。

这种基于模型平滑技术的学生-老师框架后来广泛应用于多种优秀的自监督框架（如 MoCo、BYOL）中，如图 2 所示。

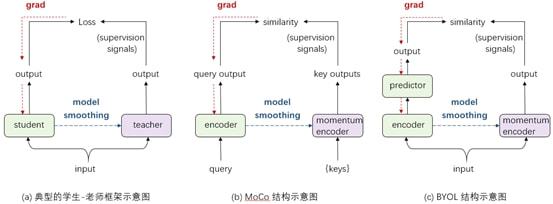
图2

什么是模型平滑？

随着训练过程的推进，学生网络不断通过梯度反向传播进行更新，我们可以得到一系列不同版本的学生网络（每次更新对应一个版本）。

我们将所有版本的学生网络称为历史学生模型。模型平滑技术即是希望基于所有历史学生模型来得到一个平滑版本的老师模型。

时序滑动平均（Temporal Model Smoothing，简称 TMA）是当前最主流的一种模型平滑技术。简单来说，如图 1 所示，时序滑动平均的核心思想是将所有历史版本学生网络参数的加权平均作为老师网络的参数。

在时序平滑过程中，每个学生网络被作为一个整体进行处理，即一个学生网络中的所有层都将参与加权平均过程，且所有层共享相同的加权权重。

随着训练时间的增加，模型会变得越来越强，旧的模型与现有模型的差距越来越大。

如果为不同时间版本的学生模型分配不同的权重，为时序上较近的模型分配更高的权重，时序上较远的分配较低的权重，便得到了一种特殊的时序平滑机制，即指数滑动平均（Exponential Moving Average，简称 EMA)。

经典的半监督 Mean Teacher、FixMatch 等，以及自监督框架 MoCo、BYOL 都使用了 EMA 这种时序模型平滑技术来得到稳定可靠的老师网络。

为什么需要模型平滑？

自监督方法 MoCo 和 BYOL 中都注意到，如果我们去掉模型平滑，模型将无法学习到有效的特征表示，产生糟糕的性能表现。出现这种现象的原因是什么呢？

为了更好的理解模型平滑在其中发挥的作用，我们从两个角度对训练过程进行了统计分析：即，相邻两个训练周期（epoch）之间老师模型的参数的差异，以及老师模型对同一批样本产生的监督信号的差异。

我们使用均方误差（Mean Square Error，MSE）来衡量差异的大小，详见图2。其中 None 表示不使用任何模型平滑技术。为了方便可视化，我们使用 log 函数对纵坐标进行了缩放。

图3 相邻 epoch 间老师模型参数的MSE（左）以及监督信号的MSE（右）

观察图 3，我们可以发现当不使用任何模型平滑技术时，相邻 epoch 老师模型参数以及产生监督信号的 MSE 始终维持着一个比较高的值，说明此时模型产生的监督信号十分不稳定，模型抖动较大，且没有明显的收敛趋势。

而当使用了 TMA 或 SE（我们的方法，下文将介绍）后，可以观测到无论是老师参数 MSE 还是监督信号 MSE 都取得了明显较低的值，且在逐步降低，说明此时模型产生的监督信号相对稳定，且模型正在平稳收敛。

因此我们可以得出结论，模型平滑技术可以有效地确保监督信号的稳定性，促进模型的收敛。

2

新的平滑方式——空间集成

基于时序的 EMA 平滑是当前最为主流的模型平滑方式，鲜有工作聚焦于探索不同的平滑方式。本文中，我们从新颖的空间平滑角度出发，提出了一种新的模型平滑机制“空间集成”（Spatial Ensemble，简称 SE）。

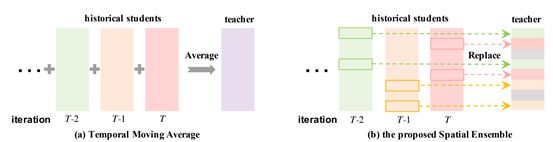
图 4 时序滑动平均和空间集成示意图

如图 4 所示，TMA 对历史学生模型的参数进行加权平均来更新老师模型的参数。SE 从另一个角度实现了模型的平滑。

具体来说，在每次更新过程中，老师网络随机挑选一部分网络子结构，并将挑选出的子结构的参数直接更新为学生网络对应子结构的参数，而本次更新过程中未被挑选出的子结构参数保持不变。

经 过多次空间集成更新，老师网络的不同子结构可能源自于不同历史学生模型。

以一种更为形象的方式来说，空间集成将历史学生模型的不同子结构“缝合”成了老师模型，从而产生了“空间集成”效应。这也是我们方法名称的由来。

时空平滑

再进一步，我们注意到时序平滑和空间集成存在天然的互补性，且可以很自然的结合在一起，从而得到一种新的模型平滑机制——时空平滑（Spatial-Temporal Smoothing， 简称 STS）。图 5 横向对比了 TMA、SE 和 STS 三种平滑机制。

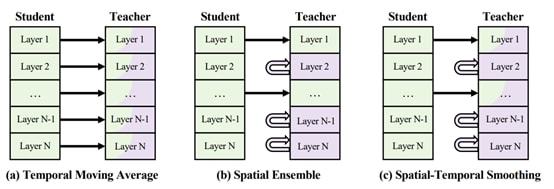
图 5 三种不同的模型平滑机制

TMA 将整个网络作为一个整体，逐层进行进行加权平均操作。空间集成随机将老师网络的部分子结构替换成学生网络中对应的子结构，而保持其他子结构不变。

STS 结合了 TMA 和 SE：类似 SE，STS 同样随机令部分子结构保持不变，但对于其他需要更新的子结构并不是直接替换成学生网络的子结构，而是借助于 TMA 进行更新。

数学形式

假设 和 表示老师网络和学生网络的参数，且都可以表示为 n 个单元（units)，即 ,且 。依据 SE 采用的空间粒度，一个单元可能对应一个网络层，一个特征通道，或者一个神经元。

因此SE可以表示为以下形式：

其中， 是一个服从伯努利分布的二值变量。如果 ，表示该单元保持不变；如果 ，则表示该单元将被替换成学生网络中的对应单元。

所有 是彼此互相独立的，即每个单元独立判断保留或替换。 越大，意味着越高的保留频次以及更多的期望保留单元数。

类似地，我们可以将 STS 表示为以下形式：

其中 表示 TMA 中的动量（momentum）。 控制了 TMA 模型平滑的程度， 越大平滑效应越强。

在特定情况下，STS 能够退化成 SE 或 TMA。例如当 时，STS 退化成了 SE。当 时， ，STS 将退化成 TMA：

3

实验分析

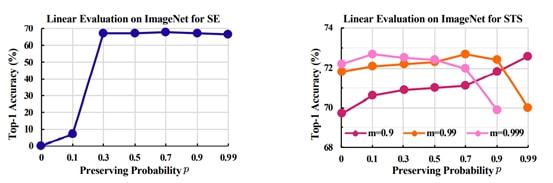
图 6 不同超参设置下，SE 和 STS 在 ImageNet 数据集上的线性评估结果

图 6 展示了不同超参设置下，SE 和 STS 在 ImageNet 数据集上的线性评估结果。

观察左图我们可以发现，当 p=0 时，即模型平滑效应不生效时，模型性能表现十分糟糕，说明没有学习到任何有效的特征表示。而随着 p 的增大，模型性能呈逐步上升，说明了 SE 能够作为一种有效的模型平滑方式。

如右图所示，STS 通常能够取得优于 TMA（对应 p=0）的性能，说明了 SE 和 TMA 的互补性。此外我们可以观察到一个有意思的现象：随着m 的增大（减小），模型通常在相对偏小（偏大）的 p 值处取得最佳性能。

这些结果反映了模型平滑对基于学生-老师框架的自监督模型的重要性。

下图展示了我们的方法与其他 SOT A 方法在 ImageNet 上线性评估结果的比较。

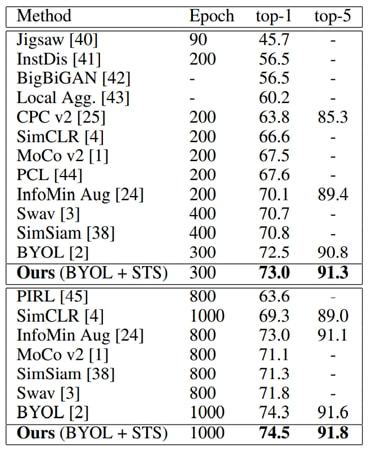
图7

此 外，我们还观察到，基于 STS 学习到的特征在 ImageNet-C 数据集上表示呈现出对数据噪声（data corruption）更强的鲁棒性。

ImageNet-C 是一个常用的评估模型对数据噪声鲁棒性的数据集，其中包括 15 种不同的数据噪声类别，且每种类别包含 5 种不同的噪声强度，即共计 75 种数据噪声。

图 8 左展示了数据集中的几种典型噪声，从上到下依次是 defocus blur, pixelate, fog, 和 spatter。每张图左下角 展示了 STS 相比 TMA 带来的性能提升。对所有 75 种数据噪声，STS 平均能够带来约 1.5% top-1 accuracy 提升。

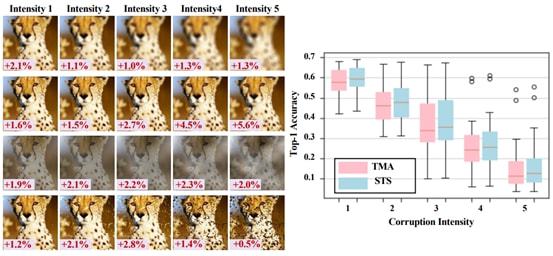
图 8 ImageNet-C 数据集上噪声鲁棒性验证

此外，我们观测到 STS 学习到的特征具有良好的泛化性，并在下游检测任务 VOC 物体检测数据集上展现出良好的性能。

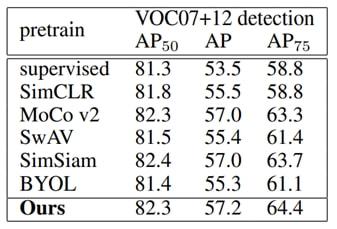
图 9 物体检测任务上的迁移学习

4

总结

模型平滑技术保证了学生-老师框架中监督信号的稳定性，有效促进模型收敛，在半监督尤其是自监督方法中起到了十分关键的作用。

我们提出了一种新颖的空间平滑方式 SE，其能够取得与经典的时序平滑方式 EMA 可比的自监督性能。

SE 与 EMA具有良好的互补性，据此我们提出了一种时空平滑机制 STS。STE 能够取得更好的自监督效果，并且具有良好的泛化性和鲁棒性。